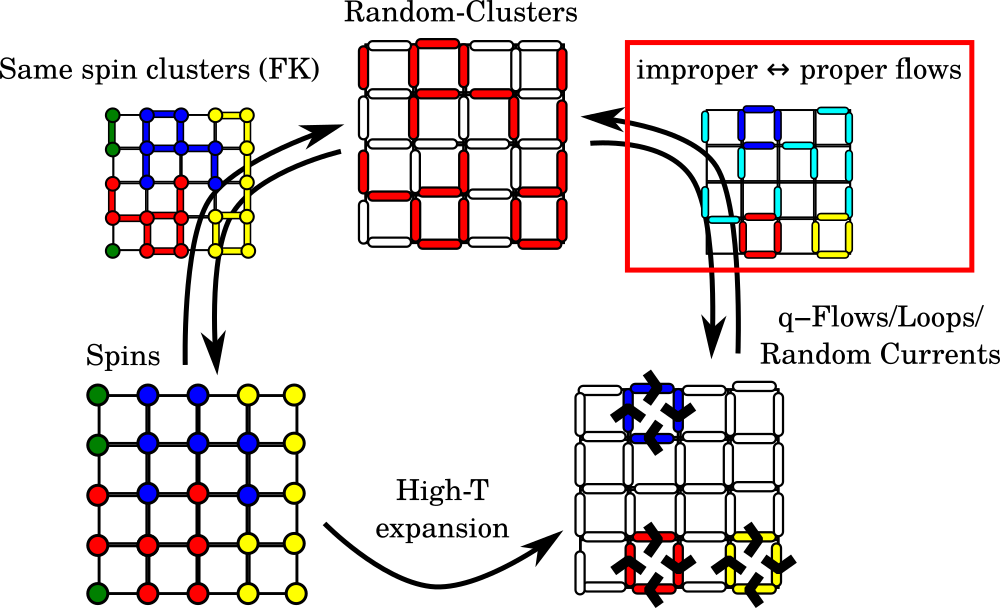
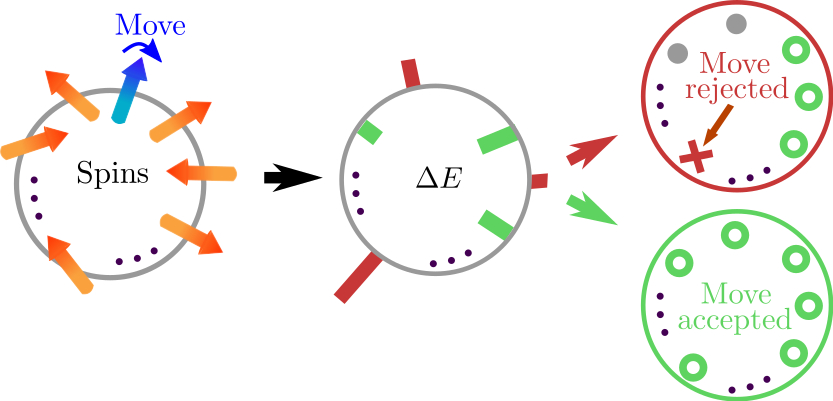
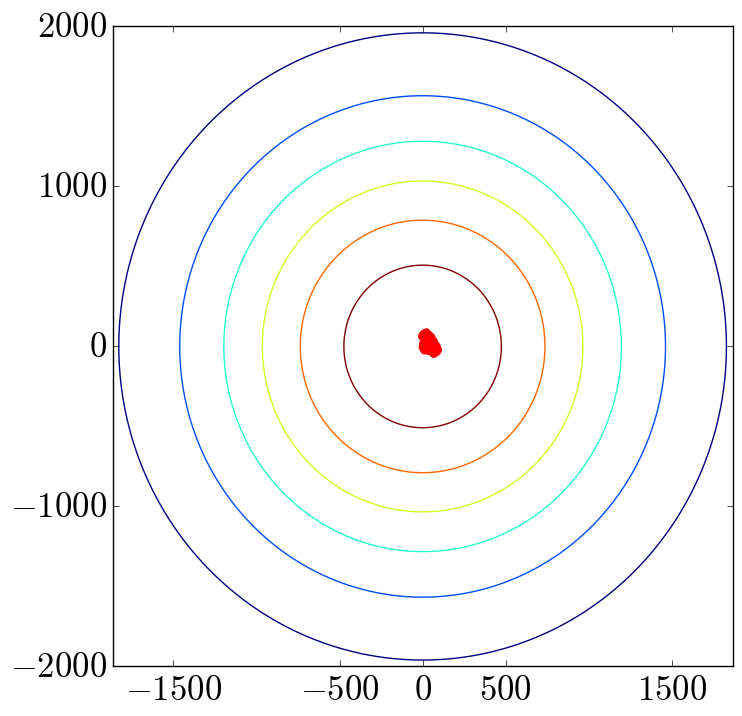
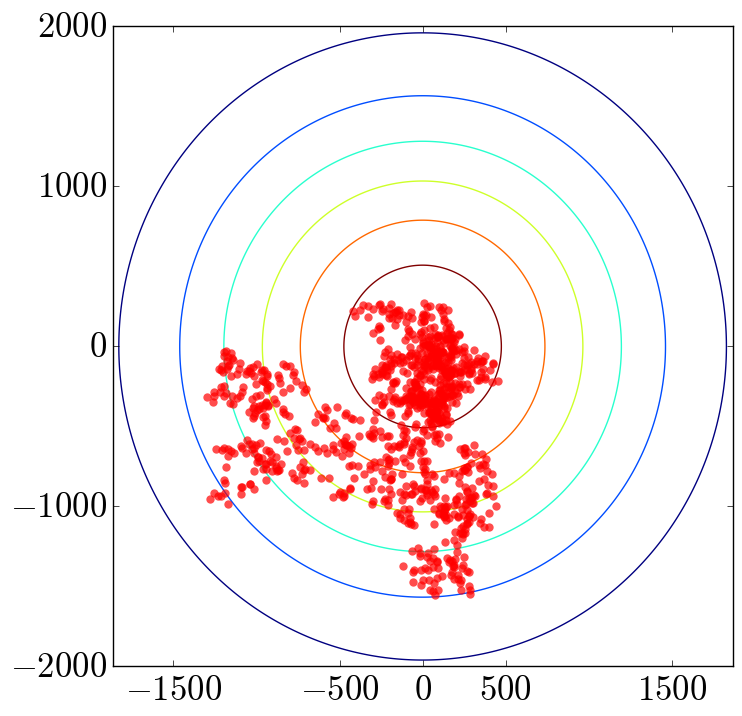
Manon MICHEL

I am a CNRS researcher (CR) at the LMBP (Laboratoire de Mathématiques Blaise Pascal - UMR 6620) at Université Clermont - Auvergne (France) in the Probability, Analysis and Statistics team.

My research lies at the intersection of theoretical physics and mathematics. It covers a broad thematic spectrum, ranging from the study of stochastic dynamics to statistical mechanics, while also developing new algorithms in sampling and learning.

The research themes I address can be grouped as follows:

  • Statistical Mechanics: particle systems, lattice spin systems, phase transitions, out-of-equilibrium physics.

  • Stochastic Processes: longtime behaviors, Markov processes, nonreversible processes, convergence, coupling, neural network analysis.

  • High-dimensional Simulations: computational physics, Bayesian inference, Monte Carlo algorithms, unsupervised learning methods, generative models.

You can find an up-to-date list of my publications on Hal or Google Scholar.

pic pick pick pick


News

I am co-organizing with T. Swinburne (CNRS/CINaM) an upcoming 3-week program on Probabilistic sampling for physics: finding needles in a field of high-dimensional haystacks , September 4th - September 22nd 2023 at Institut Pascal (Saclay, France) . More info here.


Projects

Logo Susa For more info on the ANR-JCJC project SuSa I am coordinating please visit the official website !


Gallery

Research works

Loop-Cluster Coupling and Algorithm for Classical Statistical Models

LC coupling

The q-state Potts model plays a major role in the study of critical phenomena, mostly thanks to the different representations one can use for its description, the spin, Fortuin-Kasteleyn (FK) and loop representations. Historically, a coupling between the FK and spin representations was derived and was successfully and extensively used for theoretical and numerical purposes for forty years. In the absence of any coupling with the other representations, the loop one has still to be considered independently, whereas it allows direct access to the magnetic susceptibility or correlation quantities. Following an approach based on the decomposition of random clusters into loop ones, our work now completes the construction of this missing theoretical and numerical link and ties together the three representations by the introduction of a joint-model between the FK and loop ones.
Clock Monte Carlo: From computational complexity to energy extensivity

Clock Monte Carlo

This general method allows for an efficient information extraction and a constant-time complexity by only relying on the separation of the energy into its independent components. The obtained acceleration is however limited by the disorder and frustration present in the system and we show how it is directly ruled by the energy extensivity nature, regardless of the system's peculiarities. As previous reduction methods can be seen as special examples of this new class, this work asks the question whether the complexity of energy landscapes is a strict bound for any random walk's complexity.
Forward event-chain Monte Carlo: taming randomness by symmetry exploitation

Metropolis Monte Carlo Bouncy event-chain Monte Carlo Forward event-chain Monte Carlo

Since fifty years, the conservation of the equilibrium probability distribution in Markov chain Monte Carlo was ensured by the artificial introduction of the reversibility symmetry (left). During the 2010s, non-reversible Markov chains (right), breaking the reversibility symmetry, were introduced and shown to be faster. We show how they still rely on an artificial local symmetry and how by replacing this artificial symmetry into a real one (invariance by rotation aroung the energy gradient) we obtain a dramatic acceleration (right). This generalized non-reversible MCMC is called the Forward event-chain Monte Carlo method.

Some historical simulations

2nd-order phase transition in bidimesional Ising spin systems (Onsager, 1944)

config

Buffon's experiment (1733)

Buffon Buffon's experiment